Fair Game（國三下機率）

Fair Game（國三下機率）

　　在機率的世界中，Joe叔叔對於「公平」這兩個字的印象特別深刻。例如題目會出現公平的骰子或公平的銅板。對於喜歡到香腸攤去打香腸的Joe叔叔來說最擔心的莫過於老闆用的骰子不公平了！當然香腸攤的老闆也非等閒之輩要比賽之前，老闆都會先問Joe叔叔要比大還是比小來以示公平！（不過平手則算莊家也就是老闆贏喔！這個規則則對客人不利。）

　　在美國留學時曾經到過大西洋賭城去玩過的Joe叔叔，對於賭城一些特別的規則感到十分的有趣，例如每張賭桌的賭注有最高的上限（例如一次下注最多不能超過xxx美元，這個限制對莊家－也就是賭場有利）

　　看看以下的例子就可以發現Fair Game的觀點解題有多麼快了！

例：甲乙兩人猜拳（剪刀石頭布）如果分別出剪刀、石頭和布的機率都一樣（各三分之一的意思拉），若兩人出一樣的就算平手（沒輸沒贏），請問甲獲勝的機率是多少？

　　這種題目或許有的小朋友會用所謂的樹狀圖來解題

　　不過事實上只要考慮甲乙兩人平手的機會是（甲乙出拳的所有組合可能性是9種：例如甲出剪刀乙出石頭；而平手的情況只有3種：例如甲出剪刀乙也出剪刀）

　　扣掉平手後剩下的機率為，而這個猜拳的遊戲並沒有特別偏袒甲或乙，因此甲勝乙或乙勝甲的機率應該一樣，所以把平分。

　　結論：甲勝乙的機率＝；乙勝甲的機率＝；平手的機率＝

 

　　如果小朋友或家長覺得剛剛的例子太簡單，那Joe叔叔來介紹下面這一題

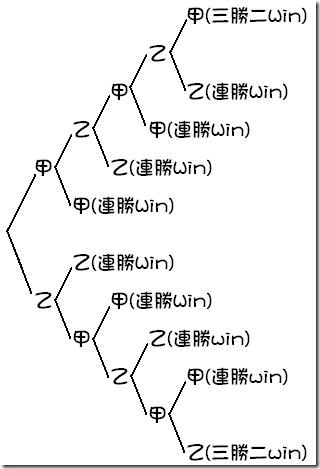
例：甲乙兩人比賽撞球，第一個連勝兩場或先勝三場者贏的比賽，請問甲贏得比賽的機率為多少？

　　如果這一題要用剛剛的樹狀圖解題那可有得畫了：

　　可是如果用Fair Game的觀點那麼，馬上就可以寫下答案：（因為遊戲規則中並沒有特別偏袒某一方）

 

　　如果這樣的題目還是覺得不過癮，那我們來看下一個標準的題型：

例：投擲一粒公正的骰子兩次，請問第二次的點數不小於第一次的點數的機率是多少？

　　分別丟兩次骰子，那麼所有的組合為6×6＝36種可能性。

我們可以把所有的組合分成以下三類：

（A）第二次的點數＝第一次的點數

（B）第二次的點數＞第一次的點數

（C）第二次的點數＜第一次的點數

　　其中（B）和（C）出現的可能性應該是一樣多：例如出現第二次丟2點＞第一次丟1點，就一定會出現第一次丟2點＞第二次丟1點！

　　因此只要把（A）的所有可能性算出來剩下的平分給（B）和（C）就O.K.啦！

（A）的可能性包括：兩次都出現1點、2點、3點、4點、5點、6點共6種組合，因此兩次點數相等的機率是。

（B）的機率＝（C）的機率＝。

　　所以回到題目所說的：第二次的點數不小於第一次的點數的機率是多少？（不小於就是大於等於喔！）

　　那麼我們只要把（A）＋（B）＝，這樣算是不是比慢慢數要快很多呢？