等差數列三斧頭之一號公式(國二下)
等差數列的定義就是相鄰兩項中後項減掉前項為一個固定數,這個固定數就叫做「公差」。如果用數學符號來表示就是數列:
看起來這麼簡單的定義,在月考的時候卻常常愛考小朋友判斷哪些數列是等差數列喔!
看看下面幾個等差數列的例子:
(A)8,8,8,8,8=>Joe叔叔把這種都是一樣的數列叫做「心臟停止」,雖然公差是「0」,可是它絕對還是等差數列喔!
(B)=>看起來這些有開根號的數怎麼會是等差數列呢?其實只要做一些化簡就會一目瞭然囉!
(C)=>整個數列都是未知數看起來有點怪怪的!不過檢查一下就會發現它是等差數列。
(D)=>這個數列相信很多小朋友如果來不及就會猜它不是等差數列,其實經過有理化後:
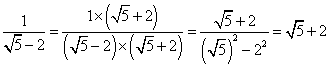
看看下面幾個不是等差數列的例子:
(A)1,-1,1,-1,1=>這個數列看似有規律(振盪數列),可是卻不是等差數列,不相信檢查一下:-1-1=-2(第二項減第一項),但是1-(-1)=2(第三項減第二項),相鄰兩項沒有固定的公差就不是等差數列!
(B)=>這個數列則是常常騙倒一堆小朋友的題目喔!這個規律到不行的數列其實兩項之間的差通通都不一樣!例如:
(第二項減第一項),而
(第三項減第二項),所以它當然不是等差數列囉!
如果嫌上述幾個例子都很容易算出來,那我們來看看幾個用未知數表示的:
例:如果a、b、c、d四個數成等差數列,那麼以下的數列也都是等差數列:
(A) 順序倒過來也會是等差:d、c、b、a(而且新的公差就會是原本的相反數)
(B) 同加一個固定數也是等差:a+5,b+5,c+5,d+5(而且公差不變喔)
(C) 同減一個固定數也是等差:a-3,b-3,c-3,d-3(而且公差不變喔)
(D) 同乘一個數還是等差:7a,7b,7c,7d(新公差=7×原本的公差)
(E) 同乘-1也是等差:-a,-b,-c,-d(新公差=(-1)×原本的公差)
(F) 對應相加另一個等差數列仍然是等差:a+1,b+3,c+5,d+7(而新的公差就是這兩個數列的公差相加喔!請小朋友自己計算一下囉)
(G) a+b,b+c,c+d也是等差數列:因為a,b,c和b,c,d都是等差數列
(H) b-a,c-b,d-c也是等差數列:因為b,c,d和-a,-b,-c都是等差數列!
但是如果a,b,c,d皆不為零時,下列兩種就不是等差數列囉
(B)1×a,2×b,3×c,4×d
看完了各種等差數列的介紹,Joe叔叔推薦小朋友月考必考的一號公式
:其中
是代表第n項,
當然就是第一項也就是首項,公差就是d,而(n-1)就是兩者之間的間隔數囉!接下來看一個標準問題:
例:一個等差數列的首項是,末項是-10,公差是
,請問此數列共有幾項?
像這種知道首項末項和公差求n的題目,當然就是用一號公式囉!
另外,針對一號公式Joe叔叔在此介紹一個經典的問題,如果等差數列的第n項可表示為5n-2,請問此等差數列的公差是多少呢?
不過Joe叔叔介紹一個可以一眼看出答案的快速解法,公差就是第n項中n的係數,那就是5!答案是不是和剛剛算了半天的結果一樣呢?
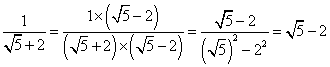
沒有留言:
張貼留言