扇形－基礎篇（平面圖形）（國二下）
從國二下的第二章開始一直到國三上結束，國中的數學課程就會進入幾何的階段，Joe叔叔看過有些小朋友雖然代數很厲害可是碰到幾何就……
因此Joe叔叔非常重視幾何，也提醒小朋友幾何不像代數，幾何的變化非常的多，隨便畫一畫就是個新的圖形，基測中難題也常常出現在幾何喔！
雖然說平面圖形在國中幾何中應該算是baby等級的內容，但是因為實在太久沒有接觸到幾何了，再加上小學學的圓周長圓面積都已經還給老師，因此Joe叔叔特別把扇形的部分整理出來，相信看過之後對於月考會出現的扇形基本題一定可以得心應手！
首先當然要搞清楚扇形的定義，它的頂點是圓心，扇形的周長是兩條半徑及圓心角所對應的弧長。因此圓心角到底是幾度就成了最重要的課題了！
如果題目已經給我們圓心角，那小朋友只要算出這個扇形到底是幾分之幾圓其他扇形弧長和扇形面積就用圓周長和圓面積的等比例下去算就O.K.了！
例：有一個扇形已知其圓心角是60度，半徑是12，求扇形的弧長和面積？
當然幾分之幾圓可以用以下的公式來算：
根據這個公式就可以算出這個扇形是
只不過有時題目會故意要小朋友求扇形周長（而非弧長），因此小朋友必須要把算出來的扇形弧長再加上兩條半徑才是正確答案喔！
扇形周長＝
上述的例子很簡單因為題目已經告訴我們圓心角了，在月考的時候老師常常是把題目反過來出，也就是給小朋友扇形的弧長、周長或扇形面積來反求圓心角，甚至從扇形周長求扇形面積的變化題！總之，不管題目怎麼變小朋友只要記得Joe叔叔講的，先算幾分之幾圓就對了！
例：已知一扇形的面積是
乍看之下，怎麼從扇形面積一下子就跳到扇形周長呢？反正Joe叔叔說過先求幾分之幾圓就對了！
所以這個扇形的圓周角就等於
最後我們來看看扇形在同心圓上的一個基本變形：
例：下圖中是一個同心圓所截出來的扇形，半徑分別是6和10，請問斜線部分的周長和面積各是多少？
首先我們只要弄清楚原來白色的小扇形和整個大扇形的圓心角都一樣是120度（也就是
斜線面積
＝大扇形－小扇形＝
斜線周長＝大扇形弧長＋小扇形弧長＋2×（大圓半徑－小圓半徑）
＝
＝
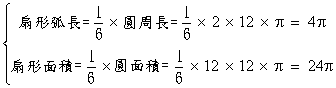
沒有留言:
張貼留言