兩點之間(勾股定理)

兩點之間(勾股定理)

上國中後變得認真許多的James居然這次數學考試有一題勾股定理的題目寫錯了！（這還是Joe叔叔講義中有的題目耶？！）

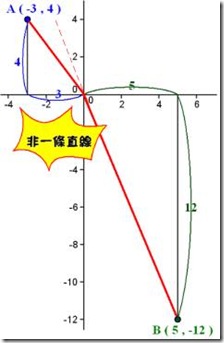
題目是甲從原點出發向西走3單位、向北走4單位，乙也從原點出發向東走5單位、向南走12單位，請問兩人最後相距多少單位？

一開始Joe叔叔不太高興（最近心情本來就不太好的說），看到小朋友居然連講過的題目還寫錯（James平時的數學是蠻不錯的），頓時有點不太高興。冷靜下來的Joe叔叔（這也是Joe叔叔的優點，雖然鬱卒還是可以立刻清醒過來，算理智型的嗎？），問James到底是怎麼錯的？James一臉無辜的說：我就分別用五虎將（Joe叔叔教的特殊直角三角形三邊長例如：5、12、13），很快就心算出甲到原點距離5單位，乙到原點距離13單位，我直接把兩個距離加起來就是答案了，心理很高興就馬上給它寫下去了！

聽完James的答辯，Joe叔叔立刻知道James是中了陷阱，James所說的都沒錯，可是最後犯錯的地方就是把甲到原點的距離加上乙到原點的距離，就自以為那就等於是甲到乙的距離了！

其實如果甲乙和原點三點共線的話，James的作法也是可以的, 只不過出題老師的用意顯然不僅於此！如果三點不共線的話，根據小學所教過的三角形兩邊之和會大於第三邊（甲、乙和原點這三個點可形成三角形的三頂點喔！），那麼甲到原點的距離+乙到原點的距離就會大於第三邊（甲到乙的距離）！雖然上述的這個性質到國二下會再教一次不過現在的小學教材也的確有教過喔（Joe叔叔還請非常有趣的童軍繩助教示範這個性質給小學生看過呢！）

所以正確的做法應該是把甲和乙的座標標出來（例如甲就是(-3,4),而乙就是(5.-12)）然後再用兩點間的距離公式算出甲乙之間的直線距離！（這也是勾股定理的應用喔）就是正確答案了！

說完落落長的正確解法和觀念後，當然也要講一個小故事加強小朋友的印象囉！據說俄國有位皇帝，當大臣正在七嘴八舌討論究竟即將開挖的運河的路線應該怎麼規劃時，這位自以為聰明的皇帝看了不耐煩，就叫人拿了一把長尺和筆，在地圖上把運河的起點和終點間畫了一條直線！ 接著就說兩點之間直線是最短距離不是嗎？照這樣挖就對了！